

Teknolojinin yanı sıra geçmişten günümüzde kadar olan süreçte de günlük hayatımıza olan tesiri büyük. Günümüzde ziraî alanların planlanmasından uzay istasyonlarının yörüngelerine kadar geniş bir kullanım alanına sahip. Biz de sizler için tanınan olan 10 analitik geometri formülünü listeledik.
Analitik Geometri Formülleri:
Doğrunun eğimi
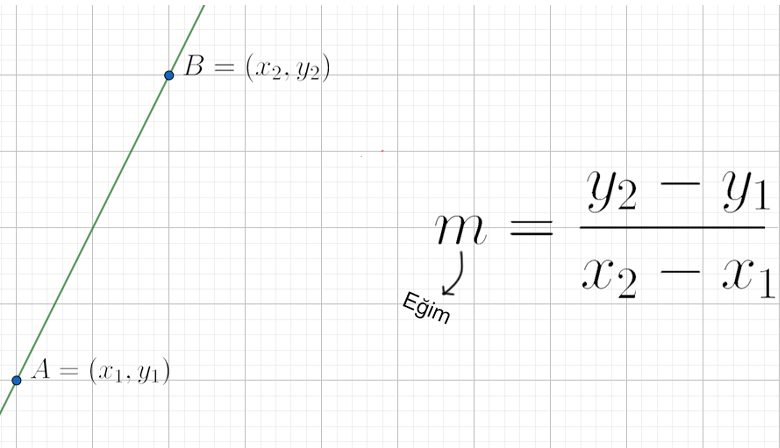
Bir doğrunun eğimi, doğrunun yataylığını ve tıpkı vakitte paha değişimini söz eder.
Gerçek ile nokta ortasındaki dik uzaklık
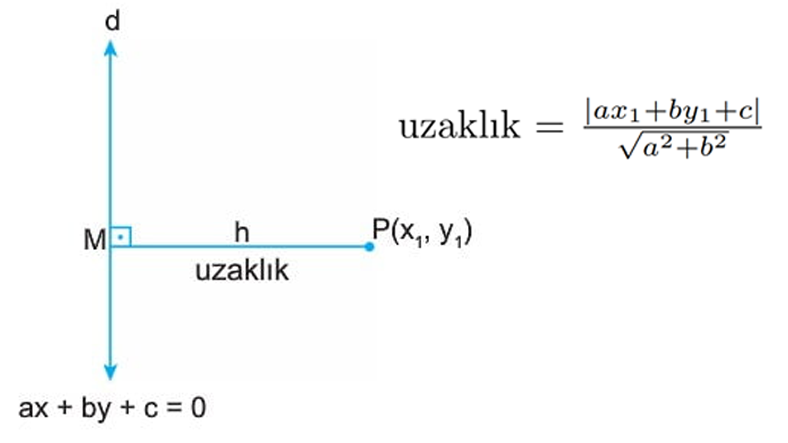
Matematikte, uzaklık birden fazla biçimde tanımlanabilir. Bu karmaşayı engellemek için dik uzaklık kullanılır. İki nokta ortasındaki uzaklıktan türetilebilen bu formül üstteki üzere söz edilir.
Eksenleri kestiği noktaları muhakkak olan doğrunun denklemi
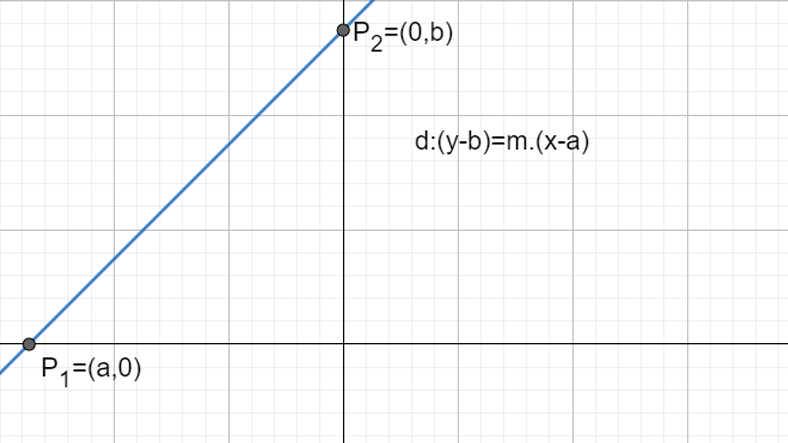
Bir doğruyu analitik düzlemde söz etmek için kimi bilgilere gereksinimimiz var. Şayet eksenlerin kestiği noktaları bilirsek doğruyu üstteki üzere tabir edebiliriz.
Yanlışsız Demeti
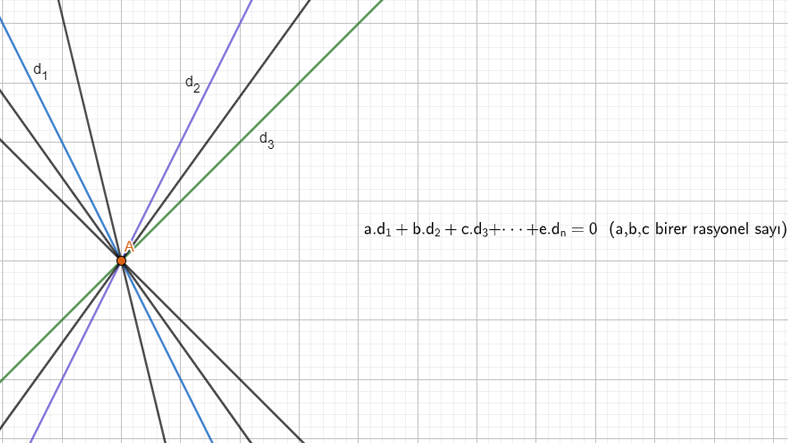
Bir noktada kesişen n tane doğrunun formülünü bilirsek, o noktadan geçen sonsuz tane yanlışsız bulmamız mümkün olur.
Kesişen iki hakikat ortasındaki açı
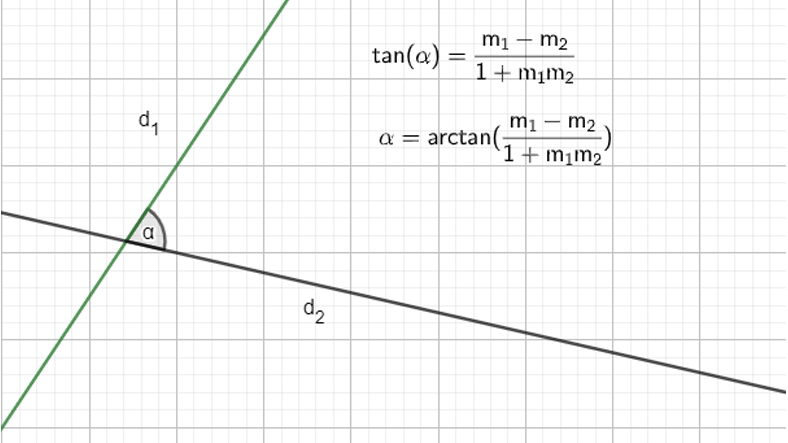
Birçok geometrik biçimi yorumlamamız sağlayan şeylerden biri de açılardır. Burada da pek çok geometrik halin temelini görüyoruz.
Analitik bir yapıyı döndürme ve öteleme
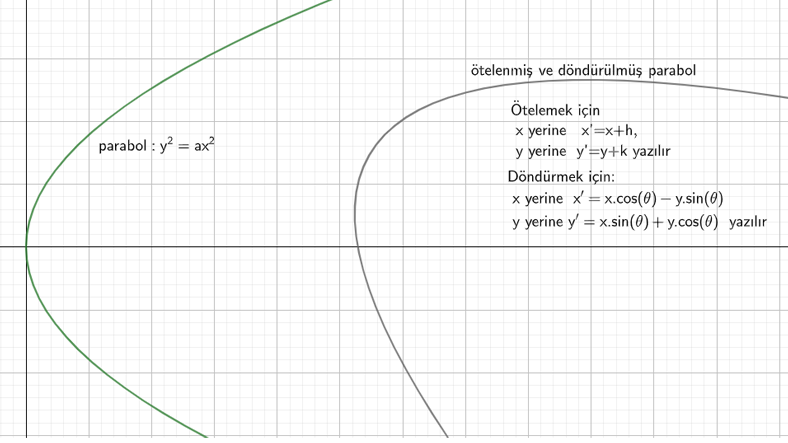
Analitik bir düzlemde söz edebildiğimiz rastgele bir şeyi istediğimiz yere öteleyebilir ve istediğimiz dereceyle döndürebiliriz.
Dörtgenin alanı
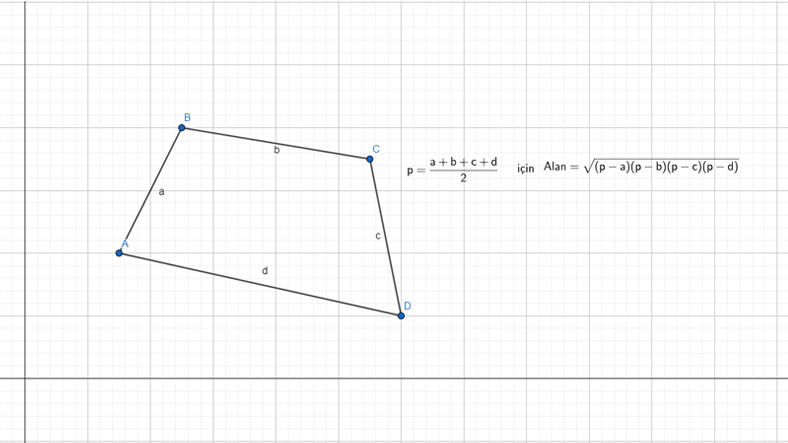
Bilhassa, arazi ölçümleri ve ziraî alanların tasarlanmasında sık sık alan hesaplarından faydalanılır. Geçmiş uygarlıklarda verimli ekin yapmak için kullanıldığı da görülmüştür.
Üçgenin alanı
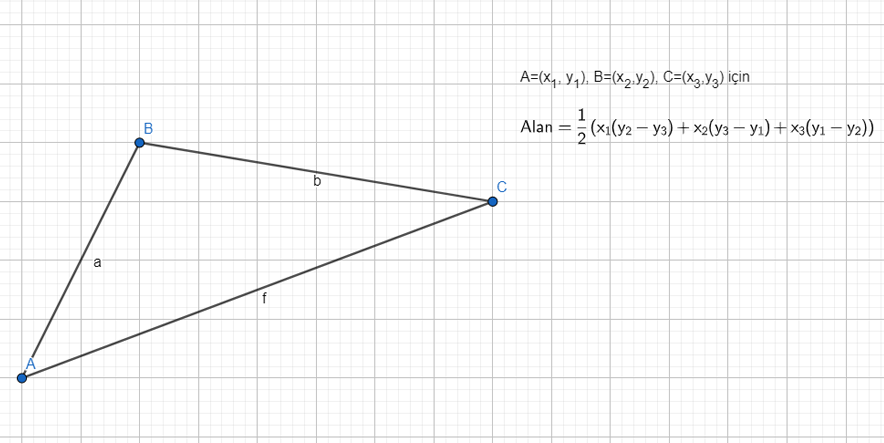
Matematikte birtakım operatörleri farklı emellerle da kullanabiliriz, üç köşesi verilen bir üçgenin alanını da multi-lineer bir işlev olan determinant ile üstteki üzere hesaplayabiliriz.
Homojen düzlemsel bir cismin tartı merkezi
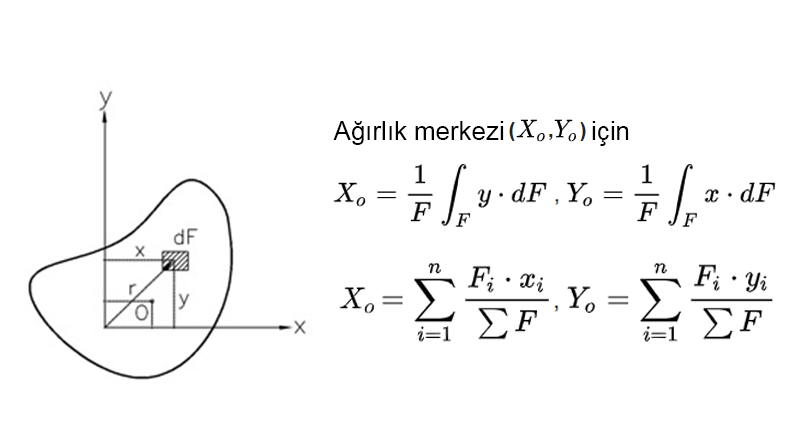
Rastgele n sayıda modülden oluşan homojen düzlemsel bir cismin, seçilen bir eksen ekibine nazaran tartı merkezi yeri olan (X, Y) noktası üstteki bağıntılar ile hesaplanabilir.
Genel konik denklemi
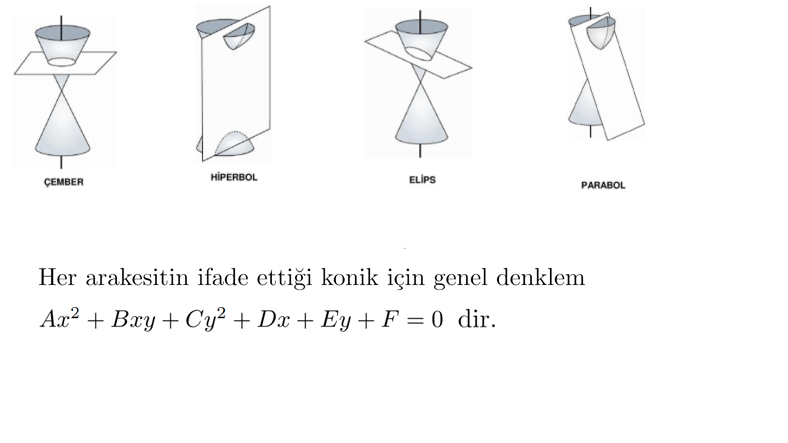
Parabol, çember, elips ve hiperbol üzere konik yapılar aslında bir koninin kesitleridir. Üstteki formül ile bütün bu konik yapıları söz edebiliriz.